1.要用9位因为2的9次方为512
2.要调整
3.要调整成10位

九位来表示
需要调整到十位!

29=512>500 所以需要9位
700>512 需要
210=1024>700 所以需要10位

9位-----2的9次方=512
需要
10位-----2的10次方=1024

9位-----2的9次方=501
需要
10位-----2的10次方=1023

2~9=512
512≥500
所以要9位

2~9=512<700
需要

2~10=1024≥700
所以要10位

1.最少需要九位二进制来表示
因为2的9次方等于512
2.需要 因为每个教职工都需要唯一的二进制位ID又因为增加了200名九位二进制不够分配所以需要调整
3.需要调整为十位二进制

对于某校需要为教职工分配唯一二进制ID的问题：

‌500位教职工的情况‌
要确定最小二进制位数
n
n，需满足
2
n
≥
500
2
n
≥500。

2
8

256
2
8
=256（不足）
2
9

512
2
9
=512（足够）
因此，‌最少需要 9 位二进制数‌。
‌增加2位后的情况‌
总人数变为
500
+
2

502
500+2=502，仍需满足
2
n
≥
502
2
n
≥502。

2
9

512
2
9
=512 仍足够覆盖 502 人。
因此，‌即使增加2位教职工，仍然只需要 9 位二进制数‌。
‌答案：‌

初始 500 人需 ‌9 位‌。
增加至 502 人后仍需 ‌9 位‌

1.最少需要九位二进制来表示
因为2的9次方等于512
2.需要 因为每个教职工都需要唯一的二进制位ID又因为增加了200名九位二进制不够分配所以需要调整
3.需要调整为十位二进制

有500位教职工需要9位二进制来表示
需要调整10位

2的9次方=512>500，需要9位二进制才能满足条件。
由于500+200=700，2的9次方=512<700，2的10次方=1024>700，所以在原来的基础上必须增加1位，需要10位二进制数才能满足ID的数量

需要九位
需要
需要十位

根据上表可以2的九次方=512>500，所以要产生500名员工的二进制ID号，需要9位二进制才能满足条件。
由于500+200=700，2的十次方=1024>700，所以在原来的基础上必须增加1位，需要10位二进制数才能满足ID的数量。

1.需要用九位
2.需要
3.需要十位

9
要
10

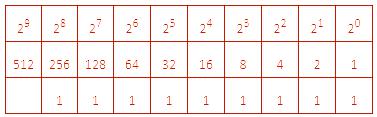
（1）根据上表可以得知2的9次方=512>500，所以要产生500名员工的二进制ID号，需要9位二进制才能满足条件。
（2）由于500+200=700，2的9次方=512<700，210=1024>700，所以在原来的基础上必须增加1位，需要10位二进制数才能满足ID的数量。

因为2的九次方=512>500，所以要产生500名员工的二进制ID号，需要9位二进制才能满足条件。
由于500+200=700，2的10次方=1024>700，所以在原来的基础上必须增加1位，需要10位二进制数才能满足ID的数量。

1.2的n次方大于等于500
2的9次方=512
所以最少需要9位来表示
2.500+200=700 2的n次方大于等于700
2的10次方大于等于1024
所以则需要调整位数为10位二进制

1.2的n次方大于等于500
2的8八次方=256（不够）
2的9次方=512
所以至少需要 9 位二进制数‌

2.500+200=700
2的n次方大于等于700
2的10次方大于等于1024
所以至少需要10位二进制数

3.2的n次方大于等于700最小的n是10
所以调整到10位合适

1.2的n次方大于等于500
2的9次方=512
所以最少需要九位来表示
2.500+200=700 2的n次方大于等于700
2的10次方大于等于1024
所以需要调整位数10位二进制

1.2的9次方等于512，大于500，所以最少用9位来表示。
2.是需要调整位数。
3.因为500+200=700，2的10次方等于1024，大于700，所以应该调整到10位。

1.2n次方》=500
九位二进制来表示
2.2n次方》=700
十位二进制

要用9位因为2的9次方为512
要调整
调成10位

1.需要九位
2.需要
3.要调整为10位

9位二进制数，因为2^9=512≥500，而2^8=256不够
要
10

1.九位,2的9次方等于512
2.需要
3.十位二进制

需要九位
需要
需要十位

1.最少需要用9位
2.需要调整位数
3.调整到10位合适

1.最少需要九位二进制来表示
因为2的9次方等于512
2.需要 因为每个教职工都需要唯一的二进制位ID又因为增加了200名九位二进制不够分配所以需要调整
3.需要调整为十位二进制

![]

根据上表可以2的九次方=512>500，所以要产生500名员工的二进制ID号，需要9位二进制才能满足条件。
由于500+200=700，2的十次方=1024>700，所以在原来的基础上必须增加1位，需要10位二进制数才能满足ID的数量。

1.2的9次方=512>500，所以要产生500名员工的二进制ID号，需要9位二进制才能满足条件。
2.由于500+200=700，2的9次方=512<700，210=1024>700，所以在原来的基础上必须增加1位，需要10位二进制数才能满足ID的数量。

9位,2的9次方=512
10位,2的10次方=1024

最少需要用9位因为2的9次方为512，大于500
需要调整到10位因为500+200=700，而2的10次方为1024

1.九位
因为2的9次方等于512
2.需要 因为每个教职工都需要唯一的二进制位ID又因为增加了200名九位二进制不够分配所以需要调整
3.需要调整为十位二进制

1.最少9位
2.需要调整位数
3.调整到10位合适